Using the Interest Rate Modeler

This chapter provides overviews of interest rate modeling and Monte Carlo System calculations and discusses how to:

• Configure setup and history data.

• Set up interest rate scenario definitions.

• Run the interest rate modeler.

Understanding Interest Rate Modeling

This section discusses:

• Interest rate modeler.

• Yield curve generator versus the interest rate modeler.

• Technical advantages of the interest rate modeler.

• Interest rate modeler integration.

Interest Rate Modeler

The Interest Rate Modeler is a flexible and powerful tool for developing and managing interest rates for asset and liability management and funds transfer pricing purposes. You can run rate scenarios, reports, and analyses in real time. Run single path scenarios and Monte Carlo scenarios. Single path scenarios include implied rates (also known as market rates), user-defined rates, and delivered rates. User-defined rates and delivered rates are also known as deterministic drift and shock scenarios. The system displays results immediately.

You can use the Interest Rate Modeler to perform the following types of analyses:

• Implied (market) rates analysis based on market rates or value sets.

• Deterministic rates analysis, including multi-interpolation drift models, shock models, and out-of-box drift scenarios.

• Monte Carlo analysis that is based on the Cox-Ingersoll-Ross model.

To use the Interest Rate Modeler:

1. Define the base currency and other base type information for the interest rate environment, such as the overall time horizon and implied forward rates.

2. Define the calendar (time buckets) for the interest rate environment.

3. Define value sets for risk-free indices or define historic index rates.

4. Define market issues.

5. Build risk-free and derived-pricing indices (including functions).

6. Define risk-free and non-risk-free term structures.

7. Define drift and shock models (deterministic rules).

8. Define Monte Carlo scenarios.

9. Define discount factors when calculating the Net Present Value (NPV).

10. Run interest rate scenarios and generate rates.

Yield Curve Generator Versus the Interest Rate Modeler

The Interest Rate Modeler and Yield Curve Generator create term structures based on pricing indices. These pricing indices can be risk-free indices based on market issues or derived indices based on other indices. This is helpful because you might want to separate the index equation definition process from how bank management uses that equation to establish product rates. For example, you might want to define the proxy for the 11th District Cost of Funds Index as your first step. Then, you can use that index to define ARM pricing behavior.

You can create interest rate environments through either the Interest Rate Modeler or the Yield Curve Generator. This table compares the two methods of creating an interest rate environment:

You should understand how the terminology in two interest rate environments map to each other. This table compares corresponding terms:

See Using the Yield Curve Generator.

Technical Advantages of the Interest Rate Modeler

The Java technology behind the Interest Rate Modeler offers the following advantages:

• The Java server processes rates online and in real time.

• The Interest Rate Modeler calculates every conceivable interest rate and maintains the rates in memory (as opposed to database tables) for optimal performance.

• The Interest Rate Modeler is platform-independent.

• The Interest Rate Modeler is completely portable among PeopleSoft Financial Services Industry applications.

• The Interest Rate Modeler is accessible from application engines or pages.

• The Interest Rate Modeler processes rates without the need for PeopleSoft Application Engine jobs.

• The Java server is easily integrated into any existing application engine.

Interest Rate Modeler Integration

The Interest Rate Modeler integrates easily into the PeopleSoft Enterprise Performance Management environment. You can build Monte Carlo and single path scenarios through the Interest Rate Modeler. You then attach interest rate models to the Model Definition and attach the model to scenarios on the Scenarios component. Scenarios are included as a parameter on run control pages for application engine jobs.

The Interest Rate Modeler is integrated with Funds Transfer Pricing. Specifically, the Interest Rate Modeler is integrated with the following functionality:

• Cash Flow application engine

  • Pricing and repricing of index rates.

  • Rate lock rates calculation.

  • Teaser rates calculation.

  • Benchmark rates calculation for behavioral models.

• Financial Calculator

  • Term structure rates for discount factor calculations.

  • Base rates for duration calculations.

• Funds Transfer Pricing

  • Cost of funds curve calculation.

  • Funds transfer pricing rates calculation.

  • Funds transfer pricing cash flow module.

• Cash Flow Modeler

  Same functionality as the Cash Flow application engine and the Financial Calculator.

• Hedge Management

  Same functionality as the Cash Flow application engine.

• Portfolio Forecast

  Same functionality as the Cash Flow application engine.

See PeopleSoft Enterprise Funds Transfer Pricing 8.9 PeopleBook.

Understanding Monte Carlo System Calculations

This section discusses:

• The database component of the PeopleSoft Monte Carlo System.

• The PeopleSoft Monte Carlo System algorithm.

• NPATH (number of paths) calculations.

Database Component of the PeopleSoft Monte Carlo System

The tables and fields in the database for value sets, market issues, and time buckets is the same for the Interest Rate Modeler environment as it is for the Yield Curve Generator environment. Models contain three numbers (a, b, and ), where a is the speed of reversion, b is the reversion rate, and is volatility. These numbers define the main formula of the IRS:

In the equation above, R is the continuously compounded short-term rate, is the length of the time bucket, and is N(0,1) random variable.

PeopleSoft Monte Carlo System Algorithm

The PeopleSoft Monte Carlo System algorithm consists of four main elements:

1. Implied rate computations.

   This part of the algorithm is the same as the forward rate computations in the single path analysis.

   The result of this step is a set of forward rates, F(t_i,t_i+1), with t₀ equal to the analysis date and each interval (t_i,t_i+1) coinciding with one of the time buckets.

2. Short-term rate computations.

   1. Each short-term rate path starts with the same value, R_k(t₀,t₁) (k=1, 2, ..., NPATH) that is equal to the value of F(t₀,t₁). Initiate along the path discount factors for each path df_k(t₀) (k=1, 2, ... , NPATH) set equal to 1. Note that df is the discount factor for each path and NPATH is the size of the current block.

   2. For each path in the block of IRA, raw rate values (R_k(t_j,t_j+1)) are calculated using the main formula of the IRS above.

   3. Compute values for discount factors along the path:

      

   4. Make the arbitrage free adjustment:

      

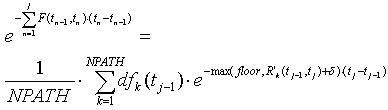
      This equation should be solved with respect to . Floor is a small positive number (for example, .00001).

      The final result for the short-term rate is:

      

   5. Repeat steps b, c, and d for all time buckets.

3. Risk-free index calculations.

   To compute all risk-free indices, the PeopleSoft Monte Carlo System uses the following IRS formulas:

   

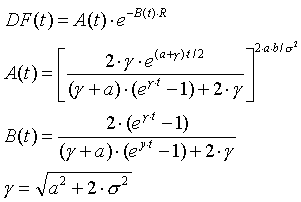
   These equations show how to compute the discount factor for any maturity t for given short-term rate R and set of parameters a, b, and . Therefore, you can use the same equations that you used in the single path analysis to solve for the values of the risk-free indices.

4. Derived index calculations.

   The PeopleSoft Monte Carlo System computes derived indices in exactly the same way that they are computed for the single path analysis.

Note. The PeopleSoft Monte Carlo System computes short-term rates for all paths in the block simultaneously. It computes all other indices path by path.

NPATH Calculations

PeopleSoft Monte Carlo System runs NPATH calculations based on the number of paths (NP) that the user wants to create and the maximum block size (BS).

If BS NP, then NPATH=NP.

Else if BS*p=NP for some p>1, then the Monte Carlo Simulator should create p blocks of size BS.

Else if BS*2>NP, then the Monte Carlo Simulator should create two blocks. The size of the first block is and the size of the second block is .

Else the Monte Carlo Simulator should create p blocks of size BS, where p is such that BS*(p+2)>NP and BS*(p+1)<NP. In addition PeopleSoft Monte Carlo System should create a block of size and a block of size .

The symbol means biggest integer smaller then X.

Configuring Setup and History Data

This section discusses how to:

• Define rate parameters for currency definitions.

• Define time parameters for currency definitions.

• Define time buckets.

• Define value sets.

• Define historic interest rates.

Pages Used to Configure Setup and History Data

Defining Rate Parameters for Currency Definitions

Access the Currency Definition - Rate Definition page.

To define rate parameters for currency definitions:

1. Select the Base Currency check box to indicate this is base the currency definition.

2. Select the currencies to include in the currency definition.

3. Enter the long-term target interest rate that is beyond the specified term in the Implied Forward Rate field.

4. Enter the period of time in which the distance between the interest rate at the end of the specified term and the implied forward rate decreases twice in the Half Decay Period field.

Defining Time Parameters for Currency Definitions

Access the Currency Definition - Time Definition page.

The system automatically displays the currencies that are entered in the Rate Definition page.

To define time parameters for currency definitions:

1. Enter the length of the overall scenario in the Overall Scenario Length field.

2. Enter a value in the Short Rate Length field.

   The system uses this value to compute the rates at the end of the overall scenario length. The short-rate length must be greater than or equal to the overall scenario length but less than or equal to the longest maturity of the risk-free index. When you run Interest Rate Modeler for the scenario, the system guarantees that the short-term rate meets this criteria. If the short-term length that you entered extends beyond these limits, the system adjusts the short term rate to the last valid rate that occurs within the limits.

3. Select the unit of measure for the Overall Scenario Length and Short Rate Length in the UOM (unit of measure) field.

   Values are Year(s), Month(s), or Day(s).

Defining Time Buckets

Access the Time Buckets page.

Use the Time Segment group box to set up the start, cycle, and end of each time segment for the time buckets. Each time segment builds upon the preceding one when you build out the calendar. When you apply additional time segments, ensure that you place the new segment correctly in the overall time frame.

In most cases, detailed information is required for the first year of a time set. For example, suppose that you set up the first time set (segment) into thirty daily periods. Then, you follow this time segment with eleven one-month periods, thus completing the one-year cycle. After the first one-year cycle, designate yearly periods out to perhaps five years. After five years, design time sets with five-year periods out to a desired time frame of perhaps thirty years. The choices are yours and they provide you with the flexibility to set up multiple time sets for different purposes.

To define time buckets:

1. Select the Include Start Date check box to start each time segment of the calendar with the date that you set in the Start group box.

   Clear the check box to start each time segment of the calendar with the following day's date.

2. Use the Start group box to indicate the start of the time segment.

   Select the start type. Values for the Type field are:

   Specific Date	Select to start the current time bucket on a specific date, and then enter the start date.
   Today	Select to start the current time segment today (based on the system date).
   Specific Period	This value is not supported in the Interest Rate Modeler.
   Defined by Period Above	Select to start the current time bucket when the prior bucket ends. You cannot select this value for the first time bucket. For example, if you set up the first year in monthly time buckets, this would be the first time bucket. To add another time bucket, insert a row and continue assigning time segments accordingly. Use the second time bucket to assign the second year of repricing periods into quarterly buckets and so forth. To ensure contiguous time segmentation rules, any subsequent time segment starts by default when the prior time segment ends.

3. Use the Cycle group box to indicate the frequency of a time bucket.

   Select the cycle type. Values for the Type field are:

   Use Period Definition	Select to utilize the calendar definitions of time. By using calendar definitions, you can take advantage of more sophisticated time segmentations, such as daily, weekly, and quarterly increments. Then select a Frequency.
   Relative	Select to indicate that the cycle is relative to the time segment number and that the buckets are equal in size. Then enter the number of relative days, months, or years.

4. Use the End group box to specify when a time bucket ends.

   Values for the Type field are:

   End of Next Cycle	Select to complete the time bucket at the end of the next cycle. Specify the cycle in the End Period field. When you specify Relative as the cycle type, the time bucketing scheme repeats until the time bucket encapsulates the end date on the period.
   End of Period	Select to complete the time bucket according to the selected calendar. When you specify Relative as the cycle type, time bucketing repeats until the time bucket encapsulates the end date on the period. If the time bucket does not end on the end date, the system creates a time bucket that runs up to the end date that is defined in the End Period field.
   Number of Periods	Select to complete the time bucket after repeating the cycle for a given number of periods. Then enter the number of times that the period should cycle in the Time field.

5. After you define your time segments, click the Calculate button to generate the time buckets.

   The Time Bucketing Output table appears and displays the results.

Note. When you create additional rules, scroll to the bottom of the scroll bar to ensure that your rules appear in sequence.

Defining Value Sets

Access the Value Sets page.

The system populates the Index ID, Description, and Tenor columns with risk-free indices that are on the risk-free yield curve.

To define value sets:

1. Click any of the Index ID links to access the Pricing Index Definition page, on which you can modify or create an index.

2. Enter the value set rate for each index on the page.

   The value sets can be used as the starting point for the rate environment generation and as an alternative to market issues.

3. If the risk-free term structure changes, click the Refresh button to update the grid automatically with the current risk-free pricing indices that belong to the risk-free term structure.

   The indices within a value set rule must match the indices that are defined as the “Risk Free Indices on the Risk Free Term Structure”. If these indices do not match, the calculation of interest rates fails. Therefore, when you build a new value set rule, the system automatically defines all of the necessary indices.

   The system imports all of the current risk-free pricing indices into the grid that are part of the risk-free term structure, thus eliminating the need to define an entirely new value set if the risk-free term structure changes.

Defining Historic Interest Rates

Access the Historic Index Rates page.

To define historic index rates:

1. Review the system-populated values for the Index ID and Description columns for the specified As of Date field.

   You can override any of the data that appears by default. The system indicates whether this is a derived DR or risk-free RF index and whether or not it is on the risk-free curve.

2. Enter a value in the Historic Index Rate column for each index.

Buttons that appear on this page are:

Setting Up Interest Rate Scenario Definitions

This section discusses how to:

• Define market issues.

• Define pricing indices.

• Maintain functions for derived-pricing indices.

• Define term structures.

• Define deterministic shock scenarios.

• Define deterministic drift scenarios.

• Define drift models.

• Add derived indices to drift models.

• Define Monte Carlo scenarios.

• Define discount rate curves.

Pages Used to Set Up Interest Rate Scenario Definitions

Defining Market Issues

Access the Market Issues page.

Define the market issues for the risk-free pricing indices. Market issues represent the risk-free market issues. The Interest Rate Modeler uses these rates as the baseline for calculating interest rate scenarios.

To define market issues:

1. Select the Pricing tab and enter the Market Issue Code along with the corresponding Tenor, UOM, Coupon, and Price.

2. Select the Properties tab and enter the Market Issue Code along with the corresponding Accrual Basis, Coupon Frequency, and Compounding Frequency.

When you add a new market issues rule, the new rule automatically inherits all market issue codes from the last available rule. The only set of parameters that is not available in the new rule is the price. Even though data is already available in the new rule, you can add new data and change or delete existing data.

Defining Pricing Indices

Access the Pricing Index Definition page.

Note. The fields that the system displays vary depending on the type of index that you use. Therefore, not all steps are applicable for a given type of index.

To define pricing indices:

1. Use the Risk Free Index field to specify whether the index is risk free or derived.

2. Enter the Currency Code.

3. Select an Accrual Basis.

   Values are 30/360, 30E/360, 30N/360, ACT/360, ACT/365, and ACT/ACT.

4. Select the Coupon Frequency.

   Values are Annual, Monthly, Quarterly, and Semi Annual.

5. Select the Compound Frequency.

   Value are Annual, Monthly, Daily, Quarterly, Semi Annual, Continuous, and None.

6. Enter the Nominal Tenor.

   Values are Years, Days, and Months.

7. Select the Index on Risk Free Curve check box to make all risk-free rates in this index part of the risk-free yield curve.

8. Click the Add/Edit Derived Function link to access the Index Definition page, on which you can add or edit the function of a derived-pricing index.

Maintaining Functions for Derived-Pricing Indices

Access the Index Definition page.

To maintain functions for derived-pricing indices:

1. In the Up = Down Equation group box, add or edit the function for a derived-pricing index.

2. Click OK to save the function and return to the Pricing Index Definition page.

The derived functions builder supports these operators:

• Comparisons: >, <, >=, <=, !=, ==

• Logical constants: true, false

• Logical operators: !&&(and), (or)

• Other statements: lag [#, xx], pow (x, #), IF ( )

The derived functions builder also supports the building of Upward = Downward or Upward < > Downward formulas in the calculation of the derived rate. Upward = Downward and Upward < > Downward is supported by use of IF ( ) functions.

You can use these operators to build complex derived functions such as smooth and step functions.

Examples of derived functions are:

• 0.0035 + (USD_RF_1Y[-1] * 0.75) + (USD_RF_2Y * 0.12) 0.0035 + (USD_RF_1Y[-1] * 0.75) + (USD_RF_2Y * 0.12)

• USD_DR_1[-2]

• (USD_DR_1+.0019) (USD_DR_1+.0019)

• (USD_DR_1+USD_DR_2)/2[-1] (USD_DR_1+USD_DR_2)/2[-1]

• USD_DR_2[-2]

Note. Equations are evaluated as numbers whereas the results appear as percentages. For example, the results of an equation such as 0.04+0.03 0.04+0.03 appears as 7.00 instead of 0.07.

Defining Term Structures

Access the Term Structure Definition page.

Use the Pricing Index Definition page to designate all of the risk-free pricing indices that comprise a risk-free term structure. Risk-free term structures are the base for spot and forward rates. You can build a non-risk-free (or derived) term structure by using any derived pricing indices. Both risk-free and non-risk-free term structures are available for funds transfer pricing cost of funds curves and discount-factor calculations.

Although all of the values of the risk-free term structures are static, you can change the values that define a non-risk-free term structure.

To define term structures:

1. Enter values in the Description and Currency Code fields for this term structure ID.

2. Select how you want the term structure to interpolate between pricing indices in the Interpolation field.

   Values are Cubic Polynomial, Linear, and Step.

3. Select the Risk Free Term Structure check box to create a risk-free term structure.

   Click the Auto Fill Grid button.

   The system retrieves all of the risk-free pricing indices that are indexed on the risk-free curve only and displays them in the grid that is to be included in the term structure definition. The grid is unavailable for editing. To edit a pricing index, click the Index ID that you want to edit. The system displays the Pricing Index Definition page, on which you edit that pricing index.

   Important! After changing, adding, or deleting the status of the risk-free pricing index, click the Auto Fill Grid button again to update the risk-free term structure to ensure that it contains only the risk-free pricing indices that are defined for the risk-free term structure.

4. To create a non-risk-free (derived) term structure, clear the Risk Free Term Structure check box.

   You can click the Auto Fill Grid button to populate the grid with all of the derived-pricing indices and risk-free pricing indices not indexed on the risk-free curve. Or, you can select, from these pricing indices, the specific ones that you want to include in the term structure definition one row at a time:

   1. Select a value in the Index ID field.

      You must have previously defined the index IDs on the Pricing Index Definition page.

   2. Enter the number of days, months, or years in the Tenor field.

   3. Enter the UOM for the tenor in the UOM field.

      Values are Days, Months,and Years.

   4. Select the Accrual Basis.

      Values are 30/360, 30E/360, 30N/360, ACT/360, ACT/365, and ACT/ACT.

   5. Select the coupon frequency.

      Values are Annual, Monthly, Quarterly, and Semi Annual.

   6. Select a Compounding Frequency value.

      Values are Annual, Monthly, Daily, Quarterly, Semi Annual, Continuous,and None.

The following button appears on this page:

Defining Deterministic Shock Scenarios

Access the Deterministic Shock Model page.

Use shock models to shock an underlying set of rates (implied or value set) immediately up or down by a number of basis points. You can apply shocks to risk-free indices on the risk-free term structure only. The shocks for all other indices are derived from these indices. The use of shock models is optional. You use deterministic models to generate new rate projections, which you can use to simulate cash flows. You can apply shock models when generating rates for implied, deterministic drift, and Monte Carlo scenarios.

To define deterministic shock scenarios:

1. Select a currency on which to base the model.

2. Enter the number of basis points by which you want to shift all risk-free pricing indices in the grid in the Shock Value (bp) field.

   Use this field in conjunction with the Apply Shock button.

3. Click the Apply Shock button to shift all risk-free pricing indices in the grid by the same number of basis points.

   The system populates the Delta (bps) field with the basis point shock value that you entered in the Shock Value (bp) field. You can then edit the Delta (bps) field values, if necessary.

4. Select the Use Derived Index Functions check box to base the derived indices that you shock on the explicit functions, as set up for pricing indices through the Pricing Index Definition page.

   Clear to base the derived indices that you shock on the value set.

5. Click the Get Indices button to retrieve all risk-free pricing indices that are part of the risk-free yield curve (term structure), as set on the Pricing Index Definition page.

   The system displays these pricing indices in the Shock Model Specifications group box.

6. The Shock Model Specifications group box displays all of the risk-free pricing index information for the shock model, including values in the Index ID, Description, and Tenor fields of the pricing indices that are included in the shock model.

   In the Delta (bps) field, enter or edit the actual shock in basis points that you want to apply to the index.

Defining Deterministic Drift Scenarios

Access the Deterministic Drift Model page.

Drift models are unique to deterministic drift scenarios. Drift models apply a shift of basis points to any index that you want over a period of time. You use deterministic models when you generate new rate projections, which you can use to simulate cash flows.

To define deterministic drift scenarios:

1. Enter a currency on which to base the model.

   If you update a drift model and want to change this value, you must click the Clear Drift Model link, which clears the entire model.

2. Use the Drift Model Options group box to define the rules of the drift model.

   Select one of the time buckets that was previously defined on the Time Buckets page. If you update a model and want to change this value, click the Clear Drift Model link, which clears the entire model. The system displays the start date that is associated with the selected time bucket.

3. Click the Clear Drift Model link to enter a new definition.

4. Click the Add Indices link to access the Add Derived Indices to Drift Model page, on which you can add derived indices to the drift model.

   Select the derived indices that you want to add, and then click OK.

   The system displays the Deterministic Scenario Definition page. If you update a model and want to add indices, click the Clear Drift Model link, which clears the entire model.

5. Click the View Indices link to access the Add Derived Indices to Drift Model page, on which you can view the derived indices that you have already added to the drift model.

6. Click the Define Drift Model link to view the Drift Model page, on which the system displays the interest rates that are calculated for each pricing index by time buckets.

The following buttons appear on this page:

Defining Drift Models

Access the Drift Model page.

The system displays the method that is used for the Interpolation Method. Options are Absolute, Backward Step, Forward Step, and Linear Interpolation. Click the Interpolate button to have the system automatically carry out the interpolation, and fill in the grid. Click OK to return to the Deterministic Scenario Definition page.

Adding Derived Indices to Drift Models

Access the Add Derived Indices to Drift Model page.

In the Use Index column, select the derived-pricing indices that you want to include in the drift model.

Defining Monte Carlo Scenarios

Access the Monte Carlo Definition page.

To define Monte Carlo Scenario models:

1. Enter the currency on which you base the rule.

2. Enter the long-term target rate for the short-term forward rate in the Rate of Reversion (%) field.

3. Enter a value in the Reversion Speed field, expressed in real numbers.

   Reversion speed characterizes the strength of mean reversion. The larger the number, the faster the short-term forward rate moves toward its long-term target.

4. Enter the annual standard deviation of shot-term forward rates in the Volatility (%) field.

5. To replicate the output for the Monte Carlo scenario on subsequent runs of the same scenario, specify the random seed number that you want the scenario to use in the Random Seed field.

   Monte Carlo analysis is a type of stochastic interest rate modelling, which in turn is based on generating random interest rate paths. The generation of these random interest rate paths is performed in part by a random number generator. The random seed number is one of the input parameters that the random number generator uses. Using the same random seed number in consecutive scenarios ensures that the output is the same and is therefore replicable. This is useful when you test Monte Carlo scenarios.

6. Enter the total number of Monte Carlo paths or iterations that you want the program to generate in the Number of Scenarios field.

   The purpose of the Monte Carlo analysis is to generate multiple interest rate scenarios (also known as paths). Thousands, or potentially, tens of thousands of paths are created in one run. The Monte Carlo analysis enables you to report the results of the simulation, either as a portfolio distribution or as a particular risk measure.

7. For performance optimization, enter the maximum number of Monte Carlo paths that are to be held in memory at any moment during processing in the Block Size field.

   This enables you to specify a number of paths greater than the available memory for a given machine. When you run the Interest Rate Modeler for this Monte Carlo scenario, the process commits the calculated interest rates to memory each time it completes this number of scenario iterations. The block size enables the Interest Rate Modeler to process one subset of the total number of scenarios at one time, therefore making the most efficient use of the computer's memory.

   For example, suppose that you want to perform a Monte Carlo simulation with 50,000 iterations on a machine with only 500 megabits of memory. Because 50,000 iterations worth of data probably cannot be held by the machine at one time,by specifying a maximum block size of 2,000, the 50,000 iterations is now divided into 25 blocks. Each block holds 2,000 paths, and the program holds only 1 block of memory worth of results at a time. When another program (client) requests results from a given path, the first thing that the Interest Rate Environment Server (IRES) does is to verify whether it's available in the current block. If it is available, then the results return immediately; if not, the IRES calculates a new block that contains the given path, and then returns the results.

   Note. The online Histogram and Average Path display options work only on the first block and are limited to the maximum block size.

   See PeopleSoft EPM 8.9 Installation Guide, Installing and Configuring EPM Components.

Defining Discount Rate Curves

Access the Discount Rates - Currency Discount Factors page.

In the absence of a currency code, use a yield curve to derive the discount rate. Use discount rates to calculate the NPV and durations. These calculations are performed by Financial Performance Measures (FPM), which comprises the cash flow generator and financial calculator. PeopleSoft Funds Transfer Pricing uses these to obtain durations for the funds transfer pricing rate calculation.

The discount rate creates a Currency Discount Factor curve. Discount factors are derived from the Yield Curve Engine output. FPM calls the Curve Evaluator to calculate and return the discount factors.

Note. The system applies the Currency Discount Factor curve on a product level on the Financial Calculation Rules page.

To set up discount rates:

1. Enter a Default Yield Curve Code.

2. Specify the direction of the basis point shift in the Risk Premium (+/- bp) field by placing the operand in front of the entry.

3. To specify currency-specific yield curves, first select a value in the Currency Code column to override the default curve for instruments denominated in the selected currency.

4. Select the yield curve that you want to associate with the new currency in the Currency YC (yield curve) field.

   The curve description appears in the Description column.

5. Enter the basis point margin and the direction of the margin in the Risk Premium (+/- bp) field by placing the operand in front of the entry.

   (Any number without a negative sign implies a positive shift).

Running the Interest Rate Modeler

This section provides an overview of the Interest Rate Modeler and discusses how to:

• Generate rates for single path scenarios.

• Generate rates for Monte Carlo scenarios.

Understanding the Interest Rate Modeler

Use the Interest Rate Modeler to run what-if scenarios for interest rates on both single path and Monte Carlo scenarios. Single path scenarios enable you to generate implied (market) rates and rates for deterministic drift and shock models (both user-defined and delivered). Monte Carlo scenarios enable you to generate interest rates based on a Monte Carlo definition.

After you run the Interest Rate Modeler, you can view charts and actual rates on spots, forwards, indices, and term structures through various display options for single-path and Monte Carlo rate simulations. For Monte Carlo rate simulation, you can review any single path characteristics or the scenario as a whole.

When you are satisfied with your scenario, you can attach it to a model definition.

Pages Used to Run the Interest Rate Modeler

Generating Rates for Single Path Scenarios

Access the I/R Modeler - Single Path Scenario page.

To generate rates for single path scenarios:

1. Select the date for which you want to run the model in the Analysis Date field.

2. Select the path type. Values are:

   Implied Rates	Same as base scenario with no drifts. Market rates or value sets are baseline. Rates are interpolated by step, linear, or cubic methods.
   User Defined Scenario	Deterministic drift or shock method.
   Delivered Scenario	Same as Deterministic method but with a set of delivered drift rates.

3. Select a value in the Time Set field.

   If you are running a delivered or implied scenario, the Time Set field becomes available. Select one of the time sets (time buckets) that was defined previously on the Time Buckets page.

4. Select a value in the Delivered Drift field.

   The Delivered Drift field appears only for the Delivered Scenarios path type. Select the basis point adjustment, up or down, from the delivered options.

5. Select a value in the Drift Model field.

   The Drift Model field appears only for the User Defined Scenarios path type. Select the drift model that you want to attach to the scenario. Click the Next Page button to access the Deterministic Drift Model page, on which you can view the details of the drift model.

6. Select a value in the Shock Model field that was defined previously on the Deterministic Shock Model page.

   When you run the Interest Rate Modeler, it shocks the rates in risk-free indices according to the specified number of basis points as defined in the shock model. You can click the Next Page button to access the Deterministic Shock Model page, on which you can view the details of the shock model.

7. Use the Underlying Source Data group box to select the basis interest rates to use as the foundation of the rates that you derive in the scenario.

   Derive the rates from value sets or market issues:

   1. Select one of the value sets from the Value Set field that was defined previously on the Value Sets page.

   2. Click the Next Page button to access the Value Sets page, on which you can create a new value set.

   3. Select the Use Market Issues check box to base the interest rates on market issues.

      The system displays the risk-free term structure for this currency code.

8. Select a value in the Display Selection field. Values are:

   Index Chart	Select to view a chart of rates for a specific rate type.
   Index Table	Select to view all rates for spot, forward, and index rates, and to view a table of the actual rate numbers.
   Term Structure Chart	Select to calculate and view a chart of rates for a specific term structure.
   Term Structure Table	Select to calculate the spot and forward rates for a term structure, and to view a table of the actual rate numbers.

9. Select a value in the Chart Selection field.

   The Chart Selection field appears when you select Index Chart in the Display Selection field. Select the rate type for which you want to view a chart of rates Forward Rate, Index Rate, or Spot Rate.

10. Select a value in the Index ID field.

    The Index ID field appears when you select a Index Rate in the Chart Selection field. Select the index rate for which you want to view a chart of rates.

11. Select a value in the Term Structure ID field.

    The Term Structure ID field appears when you select Term Structure Chart or Term Structure Table in the Display Selection field. From the term structures that you built, select the one that you want to calculate and view.

12. Save your entries.

    Click the Run Analytics button to generate the interest rates.

Generating Rates for Monte Carlo Scenarios

Access the I/R Modeler - Monte Carlo Scenario page.

To generate rates for Monte Carlo scenarios:

1. Select the date for which you want to run the model in the Analysis Date field.

2. Select the Monte Carlo scenario in the MC Model ID field for which you want to generate interest rates.

3. Select the value in the Shock Model field that was previously defined on the Deterministic Shock Model page.

   When you run the Interest Rate Modeler, it shocks the rates in risk-free indices according to the specified number of basis points as defined in the shock model. You can click the Next Page button to access the Deterministic Shock Model page, on which you can create a new shock model.

4. Select a value in the Time Set (time bucket) field for the time set that you want to apply to the model run.

   You defined time sets on the Time Buckets page.

   In the Random Seed field, a number appears that is set on the Monte Carlo Definition page, but you can overwrite this value. Monte Carlo analysis is a type of stochastic interest rate modeling, which in turn is based on generating random interest rate paths. The generation of these random interest rate paths is done in part by a random number generator. The random seed number is one of the input parameters that the random number generator uses. Using the same random seed number in consecutive scenarios ensures that the output is the same, and therefore replicable. This is useful during testing of Monte Carlo scenarios.

5. Enter the number of paths in the # of Scenarios (number of scenarios) field that you want the Monte Carlo scenario to run.

   One run creates thousands of paths. Monte Carlo enables you to report the results of the simulation either as a portfolio distribution or as a particular risk measure. The system displays the number that is set on the Monte Carlo Definition page, but you can overwrite this value.

6. Use the Underlying Source Data group box to select the basis interest rates to use as the foundation of the rates that you derive in the scenario.

   Derive the rates from value sets or market issues:

   1. Select one of the value sets in the Value Set field that you defined previously on the Value Sets page.

   2. Click the Next Page button to access the Value Sets page, on which you can create a new value set.

   3. Select the Use Market Issues check box to base the interest rates on market issues.

      The system displays the risk-free term structure for this currency code.

7. Complete the Display Selection field. Values are:

   Average Path Chart	Select to view the average of all paths for a specific rate type (spot, forward, or index). The Interest Rate Modeler also provides the following statistics: minimum, maximum, mean, standard deviation, and mean plus standard deviation.
   Histogram	Select to view a histogram of the rates for a specific rate type (spot, forward, or index) on a specific time set date. The histogram shows how the system distributes statistically. The Interest Rate Modeler also provides the following statistics: minimum, maximum, mean, and percentiles.
   Single Path Chart	Select to view a chart of rates for a specific rate type (spot, forward, or index) and a specific path. The Interest Rate Modeler also provides the following statistics: minimum, maximum, mean, and standard deviation.
   Table	Select to view a table of absolute rates for a specific path number.

8. Select the rate type in the Chart Selection field for which you want to view a chart of rates.

   Values areForward Rate, Index Rate, and Spot Rate.

9. Select a value in the Path Number field.

   The Path Number field appears if you select Single Path Chart or Table in the Display Selection field. Select the specific path for which you want to calculate and view a chart of rates.

10. Select a value in the Time Set Date field.

    The Time Set Date field becomes available if you select Histogram in the Display Selection field. Select the specific time set date for which you want to calculate and view a histogram of rates.

11. Save your entries.

    Click the Run Analytics button to generate the interest rates.