Understanding Actuarial Assumptions
Actuarial calculations adjust benefit amounts to an equivalent amount for a different commencement date or for a different form of payment. The conversion is based on specified assumptions about mortality, interest, and payment frequency. Together these assumptions constitute an actuarial assumption set.
Determining Actuarial Factors at Non-Integer Ages
Mortality tables include mortality assumptions for integer ages only. To determine annuity factors at non-integer ages, Pension Administration interpolates using the methodology shown in the following images.
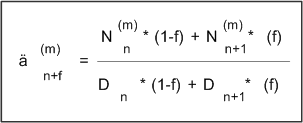
This illustration shows the formula for calculating an annuity factor at a non-integer age. In this formula:
n = integer representing whole years of age.
f = decimal representing partial year of age.
m = payments per year.
The left side of the equation is the actuarial factor for age n+f with payment frequency m.
The numerator on the right side of the equation is the commutation function N at age n+f with payment frequency m.
The denominator on the right side of the equation is the commutation function D at age n+f.
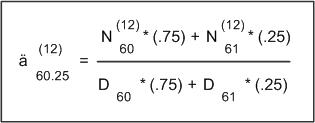
This illustration provides an example of calculating a monthly single life annuity factor for a participant at age 60.25.