Using the Statistical Matrix

This topic provides an overview of the statistical matrix.

The statistical matrix is a spreadsheet view of various statistics that you can customize to include any statistic that Quality calculates. You can display the statistics in various formats.

Some statistics may be altered through the use of non-normal distribution assessment techniques. Quality incorporates the following methods to achieve an appropriate distribution fit. Both methods use the Pearson family of distributions.

  • A test of normality, using the skewness and kurtosis of the distribution.

    If the distribution is normal at a 95 percent confidence, then the data is evaluated based on the normal assumption. If the distribution isn't found to be normal at a 95 percent confidence, then the data is evaluated using the Pearson Best-Fit family of curves. This is the recommended method if you are unsure of the distribution type.

  • Direct use of the Pearson Best-Fit family of curves.

    The routines determine the best-fit and adjust the statistics appropriately.

The set of basic statistics includes measures of central tendencies, measures of dispersion, and the other descriptive statistics, as shown in the following table:

Equation

Statistic

Alternate Equation Forms
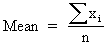
gv_7bf6_sqsy7f05

The mean is the arithmetic mean (average) of a sample.

 gv_7bf5_sqsy7f03

See References.
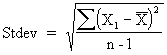
gv_7bf4_sqsy7f01

The standard deviation is the root-mean-square of a sample.

 gv_7bf3_sqsy7eff

See References.
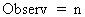
gv_7bf2_sqsy7efd

The observation is the total number of values in a sample.

None
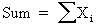
gv_7bf1_sqsy7efb

The summation is the total of all the values in a sample.

None
gv_7bf0_sqsy7ef9

The minimum is the smallest value in the sample.

None 
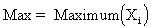
gv_7bef_sqsy7ef7

The maximum is the largest value in the sample.

None
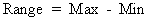
gv_7bee_sqsy7ef5

The range is the largest value minus the smallest value in the sample.

None
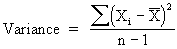
gv_7bed_sqsy7ef3

The variance is the square of the standard deviation.

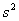
 gv_7bec_sqsy7ef1

See References.
gv_7beb_sqsy7eef

The standard error of the mean is the standard deviation of the mean. It measures the extent to which a sample mean can be expected to vary.

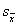
 gv_7bea_sqsy7eed

See References.
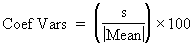
gv_7be9_sqsy7eeb

The coefficient of variation is the standard deviation of a sample expressed as a percentage of the mean. It is a measure of relative dispersion.

See References.
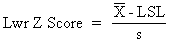
gv_7be8_sqsy7ee9

The lower Z-score is the number of standard deviations that the lower specification limit (LSL) is from the mean.

None
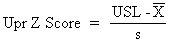
gv_7be7_sqsy7ee7

The upper Z-score is the number of standard deviations that the upper specification limit (USL) is from the mean.

None

Lwr 3 sigma = deviate at probability 0.00135

The lower 3 sigma represents three standard deviations from left of the mean.

None

Upr 3 sigma = deviate at probability 0.99865

The upper 3 sigma represents three standard deviations from right of the mean.

None

Quality calculates the twenty-fifth, fiftieth, (also referred to as the median), and seventy-fifth quartiles. The quartiles can be displayed as values and are used to graph the Box and Whisker plots.

To compute the quartiles, the system:

  1. Arranges data in ascending order.

  2. Ranks the data accordingly (1 to n).

  3. Multiplies each quartile by n+1.

  4. If the result is an integer, sets the quartile to the value of the calculated rank.

The following table shows quartile equations:

Equation

Statistic
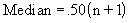
gv_7be6_sqsy7ee5

The median is the center or middle of a sample. It is the value above which there are as many values as there are below it. It is also the fiftieth percentile of the sample (Quartile 50 percent).

See References.
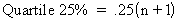
gv_7be5_sqsy7ee3

The twenty-fifth percent quartile is the point separating the lower 25 percent of the values from the upper 75 percent.

See References.
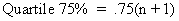
gv_7be4_sqsy7ee1

The seventy-fifth percent quartile is the point separating the upper 25 percent of the values from the lower 75 percent.
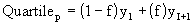
gv_7be3_sqsy7edf

where:

p is the percentile,

f is the fractional portion of the computed rank,

I is the integer portion of the computed rank.

To resolve calculated values that are not integers (for example, if the percentage lies between two values), the value is interpolated by calculating the weighted average between the two ranks.

See References.

The calculations for skewness and kurtosis use the following examples:

Equation

Statistic
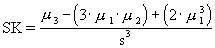
gv_7be2_sqsy7edd

Skewness measures the degree of asymmetry in a sample.
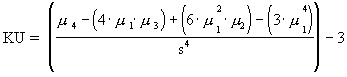
gv_7be1_sqsy7edb

Kurtosis measures the degree of peakedness in a sample.
gv_7be0_sqsy7ed9

N/A
gv_7bdf_sqsy7ed7

N/A
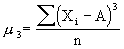
gv_7bde_sqsy7ed5

N/A
gv_7bdd_sqsy7ed3

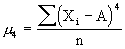
N/A

Process capability indices are industrial-accepted calculations for comparing the process output to defined specification limits. For a normal distribution, the process output is defined as :

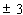
 gv_7bdc_sqsy7ed1

standard deviations from the mean. For non-normal distributions, Quality determines the Best-Fit Pearson distribution and calculates equivalent 99.73 percent deviations (at 0.00135 and 0.99865).

The following table shows equations that relate to process capability:

Equation

Statistic
gv_7bdb_sqsy7ecf

The process potential is the ratio of the process distribution to specification limits. It is the potential capability if the process was perfectly centered. This equation requires both upper and lower specifications.
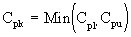
gv_7bda_sqsy7ecd

This equation represents the actual process capability. These equations account for shifts in the process center. The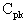

gv_7bd6_sqsy7ecb

is the lower of the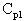

gv_7bd5_sqsy7ec9

or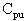

gv_7bd4_sqsy7ec7

values, or worst-case capability. In the case of a unilateral specification, the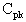

gv_7bd6_sqsy7ec5

is set to the calculated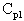

gv_7bd5_sqsy7ec3

or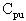

gv_7bd4_sqsy7ec1

value.
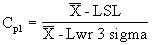
gv_7bd3_sqsy7ebf

The lower process capability represents the process's ability to perform at the LSL. This equation requires an LSL.
gv_7bd2_sqsy7ebd

The upper process capability represents the process's ability to perform at the USL. This equation requires a USL.
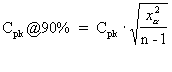
gv_7bd1_sqsy7ebb

where: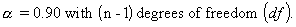

gv_7bd0_sqsy7eb9

The 90 percent confident Cpk is an adjusted Cpk based on a 90 percent confidence. The result is heavily affected by the sample size. The larger the sample size, the closer the computed value is to the actual Cpk.

See References.
gv_7bcf_sqsy7eb7

The capability ratio is the percentage that the process distribution consumes of the specification. This equation requires both upper and lower specifications.
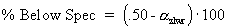
gv_7bce_sqsy7eb5

where: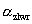

gv_7bcd_sqsy7eb3

is the area under the curve from the mean to the LSL.

The percent below specification is the estimated area under the curve to the left of the LSL. This equation requires an LSL.
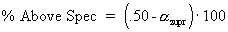
gv_7bcc_sqsy7eb1

where: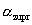

gv_7bcb_sqsy7eaf

is the area under the curve from the mean to the LSL.

The percent above specification is the estimated area under the curve to the right of the USL. This equation requires a USL.
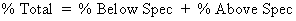
gv_7bca_sqsy7ead

The total percent out of specification is the total estimated area under the curve outside of the specification limits.

Quality uses Pearson criteria to determine the best-fit distribution for the sample. A K value, computed using the following equation, classifies the distribution as one of the following types:

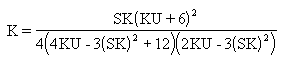
 gv_7bc7_sqsy7ea7

Pearson Frequency Curves

The following table describes Pearson frequency curves.

Type

Description

Criteria

1

Beta

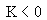
 gv_7bc6_sqsy7ea5

2

Uniform

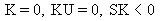
 gv_7bc5_sqsy7ea3

3

Gamma

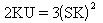
 gv_7bc4_sqsy7ea1

4

Non Central t

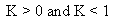
 gv_7bc3_sqsy7e9f

5

Inverse Gamma

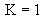
 gv_7bc2_sqsy7e9d

6

Inverse Beta

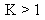
 gv_7bc1_sqsy7e9b

7

Student t

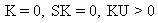
 gv_7bc0_sqsy7e99

8

Normal

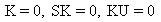
 gv_7bbf_sqsy7e97

10

Exponential

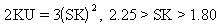
 gv_7bbe_sqsy7e95

Attribute statistics only apply to discrete data types, that is, count data. This type of data is typically associated with defect tallies.

The following table describes equations used with attribute statistics:

Equation

Statistic

Alternate Equation Forms
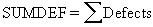
gv_7bbd_sqsy7e93

The sum of defects is the total count of all the defects in a sample.

None
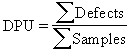
gv_7bbc_sqsy7e91

This equation represents the average number of defects per unit.

 gv_7bbb_sqsy7e8f
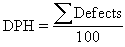
gv_7bba_sqsy7e8d

This equation represents the number of defects per 100 units.

None
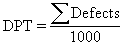
gv_7bb9_sqsy7e8b

This equation represents the number of defects per 1000 units.

None
gv_7bb8_sqsy7e89

This equation represents the number of defects per million units.

None