Appendix: Understanding Depreciation Calculations

This appendix provides an overview of depreciation calculations and discusses how Asset Management calculates:

• The begin depreciation date.

• Remaining value and remaining life.

• Yearly depreciation.

• Period allocation.

• Prior period depreciation.

• Formula-based depreciation methods.

Understanding How Asset Management Calculates Depreciation

Asset Management determines depreciation amounts using either tables or formulas. If you have a large number of assets, you will probably want to use formula-based depreciation, because this is considerably faster and uses less storage space. To help you more fully understand how Asset Management calculates depreciation, this appendix includes a discussion of how formulas are used.

When you add an asset to Asset Management, you decide the cost basis that you want to depreciate—you can include the basic cost of the asset as well as any freight and taxes that were paid. If you don’t want to include freight and tax charges in the depreciable cost basis, you can still track these charges in the Acquisition Detail page.

If allowed by the depreciation method, the cost basis is reduced by either salvage value or tax credits.

Salvage Value

You can enter the salvage value as a percentage of the cost or the actual amount. Typically, you specify salvage value when you add the asset in Asset Management. If allowed, salvage value is deducted from the cost basis for depreciation calculations. When the salvage value changes after depreciation begins, Asset Management automatically adjusts the cost basis and depreciation from that time forward to reflect the change.

Tax Credits

Tax systems such as ACRS and MACRS determine which tax credits are available in Asset Management. When you specify a Qualified Investment Code, Asset Management uses this code to determine which tax credits apply to your assets. If you fail to specify a Qualified Investment Code for any reason, Asset Management deduces the applicable code from the tax system that you elect.

If you don’t specify a tax system, Asset Management considers the date that the assets were placed in service to determine which system applies. Based on the tax system that you select and the recovery life, Asset Management derives the corresponding qualified investment code and the tax credits that available under that code, and elects the applicable tax credits for you.

If a Basis Reduction Percentage applies, the depreciable basis of the asset is reduced. The calculation is based on the Qualified Investment Code, the Tax Credit, and the Basis Reduction Percentage.

Calculating Tax Credits

Asset Management uses the Qualified Investment Code, together with the Recovery Life and in-service date, to determine the Qualified Investment Percentage—the rate that is applied to the book cost— to determine the amount that qualifies for tax credits.

The Tax Credit Percentage is derived from the Tax Credit Type, Tax Credit Code, Recovery Life, and in-service date.

The amount of the tax credit is based on the following calculations:

Book Cost x Qualified Investment Percentage = Amount qualifying for the tax credit

Amount qualifying x Tax Credit Percentage = Amount of tax credit

Cost Basis Reduction

After the amount of the tax credit is calculated, a corresponding reduction in the basis is calculated as required:

Amount of tax credit x Basis Reduction Percentage = Amount the basis will be reduced

If you dispose of the asset before it has completely depreciated, Asset Management calculates the recapture of the credit and adds it to the depreciable cost basis.

Section 179 Expense

If you elect to expense all or a portion of the cost, you should select the Section 179 Expense Taken check box on the Asset Book Definition - Tax page. You can expense assets up to an aggregate maximum of 200,000 USD per year, provided your company's gross income does not exceed the limitation that is specified by Federal tax law. Investment credits are automatically calculated based on the criteria that you enter in the Asset Book Definition - Tax Credit page.

Listed Property Assets

If an asset is considered a listed property asset for tax purposes, then the allowable depreciable basis is reduced by the percentage of business use. For example:

Business Use % = 75%

Cost = 10,000 USD

Depreciable basis = 7500 USD

Listed property is certain kinds of assets that are conducive to mixed business and personal use such as:

• Passenger automobiles under a certain weight.

• Any other property that is used for transportation such as trucks, buses, boats, airplanes, motorcycles, and any other vehicles for transporting persons or goods.

• Any property of a type that is generally used for entertainment, recreation, or amusement such as photographic, phonographic, communication, and video recording equipment.

• Any computer and related peripheral equipment unless it is used only at a regular business establishment and owned or leased by the person operating the establishment.

• Any cellular telephone (or similar telecommunications equipment) placed in service or leased in a tax year beginning after 1989.

The Depreciation Calculation Process

Asset Management performs five basic steps to calculate depreciation for an asset. It calculates:

1. The asset's beginning depreciation date.

2. The asset's remaining life and remaining value.

3. The asset's yearly depreciation.

4. The asset's period depreciation allocation.

5. The asset's prior period depreciation.

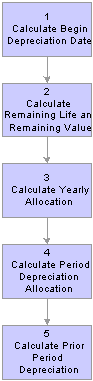
How Asset Management calculates depreciation

The following sections provide illustrative examples of how Asset Management all these calculations in a variety of different scenarios.

Note. Asset Management calculates depreciation yearly, not by month or by period. It then allocates yearly depreciation is among the year’s periods except when you select the Declining Balance depreciation method or the Declining Balance method with a switch to the Straight Line method and the monthly depreciation option is selected.

Calculating the Begin Depreciation Date

Asset Management uses two asset attributes to begin calculating depreciation:

• In-service date.

• Convention.

The combination of the in-service date and the prorate convention is the factor that actually determines when depreciation begins.

Overriding the Begin Depreciation Field

When you use the Depreciate When in Service date option, Asset Management allocates depreciation based on the date that the asset was placed in service. This option is valid only in the year that the asset is acquired.

Calculating Remaining Value and Remaining Life

Asset Management calculates remaining value and remaining life using five asset attributes:

• Begin Depr Date

• Transaction Date

• Life

• Cost

• Accumulated Depreciation

Calculations differ depending on which calculation type is used and the relationship between the beginning depreciation date and the transaction date. The following examples show how the calculation is performed for each method.

Remaining Value Calculation for Add Transactions

The following table shows data that is used in the calculation examples that follow it.

Remaining Life

When the beginning depreciation date is earlier than the transaction date:

Remaining Life = Life - (Transaction Date - Begin Depreciation Date)
60 periods - (10/1/1999 - 7/1/1999) = 57 periods 

When Begin Depr Date is equal to or later than Transaction Date:

Remaining Life = Life

Remaining Value

The following example illustrates remaining value:

Remaining Value = Cost - Accumulated Depreciation
$6000 cost − $500 accumulated depreciation = $5500 remaining value

Life to Date Calculation for Add Transactions

The following table shows data that is used in the calculation example that follows it.

Remaining Life

When Begin Depr Date is earlier than Transaction Date:

Remaining Life = Life - (Transaction Date - Begin Depreciation Date)
60 period - (10/1/1999 - 7/1/1999) = 57 periods

When Begin Depr Date is equal to or later than Transaction Date:

Remaining Life = Life

Remaining Value

The following example illustrates remaining value:

Remaining Life = Life - (Transaction Date - Begin Depreciation Date)
$6000 cost - $500 accumulated depreciation = $5500 remaining value

Calculating Yearly Depreciation

Asset Management calculates yearly depreciation using two asset attributes:

• Begin Depr Date

• Depreciation Method

Other information that is used in this calculation includes the following information:

• Adj Trans Date

• Remaining Life

• Remaining Value

Calculations differ depending on which calculation type is used: Remaining Value or Life to Date. The following examples show how this calculation is performed for each method. The base information is the same in both cases.

Remaining Value Calculation for Add Transactions

The following table introduces the data used in the calculation example that follow it.

Yearly Depreciation for 1999

Here is yearly depreciation for 1999:

Number of Periods in Year = Year End - Transaction Date
3 = 12/31/97 - 10/01/97
Percentage Depreciation for Year = Number of Periods in Year/Remaining Life
5.26% = 3 / 57
Yearly Depreciation = Percentage Depreciation for Year x Remaining Value
$289.47 = 5.26% x $5500

Life to Date Calculation for Add Transactions

The following table introduces the data that is used in the calculation example that follow it.

Yearly Depreciation for 1999

Here is yearly depreciation for 1999:

Number of Periods in Year = Year End - Begin Depr Date
6 = 12/31/97 - 7/01/97
Percentage Depreciation for Year = Number of Periods in Year/Remaining Life
10% = 6 / 60
Yearly Depreciation = Percentage Depreciation for Year x Remaining Value
$600 = 10% x $6000

Calculating Period Allocation

Asset Management calculates period allocation using three asset attributes:

• In-Service Date

• Begin Depr Date

• Transaction Date

Other information that is used in this calculation includes the following, derived from previous calculations:

• Calculation Type

• Adjusted Transaction Date

• Yearly Depreciation

• Number of Periods in Year

Life to Date calculations differ depending on whether the Depreciate When in Service option is set to N or Y. The following examples illustrate how Asset Management calculates period allocation using the Remaining Value and Life to Date calculations. All examples use the same base information.

When a remaining balance exists due to rounding in the year, Asset Management allocates that amount to the last period of the fiscal year. For example, 2000 USD to be allocated over 12 periods, periods 1 through 11 will have 166.67 each and period 12 will have 166.63 USD (2000 USD - (166.67x11).

Remaining Value Calculation for Add Transactions: Depreciate When In Service Off

The following table shows data that is used in the calculation.

Period Depreciation Allocation

Here is the period depreciation allocation:

Period Depreciation Allocation = Yearly Depreciation / Number of Periods Remaining in Year
$600 Yearly Depreciation / 6 periods = $100 per period

Remaining Value Calculation for Add Transactions: Depreciate When In Service On

The following table shows data that is used in the calculation example that follows it.

Period Depreciation Allocation

Here is the period depreciation allocation:

Period Depreciation Allocation = Yearly Depreciation / Periods from In-Service Date
Periods from In-Service Date = Year End - In-Service Date
$600 Yearly Depreciation / 10 periods from In-Service Date = $60 per period

Life to Date Calculations for Add Transactions: Depreciate When in Service Off

The following table shows data that is used in the calculation example that follows it.

Period Depreciation Allocation

Here is the period depreciation allocation:

Period Depreciation Allocation = Yearly Depreciation / Number of Periods in Year
$600 Yearly Depreciation / 6 periods = $100 per period

Life to Date Calculation for Add Transactions: Calculate When in Service On

The following table shows data that is used in the calculation example that follows it.

Depreciation Results

The following table shows yearly depreciation by period for 1999.

Remaining life is 60 periods; remaining value is 6000 USD; yearly depreciation for 1999 is 600 USD.

Calculating Prior Period Depreciation

Prior period depreciation is generally calculated only for Life to Date calculations. In Remaining Value calculations, prior period depreciation is calculated only if the accounting date occurs after transaction date.

Prior period depreciation is keyed by a derived beginning calculation date. For remaining value calculations in which the accounting date occurs after the transaction date, the beginning calculation date equals the transaction date. For life to date calculations, the beginning calculation date depends on a combination of the following items:

• Transaction Date

• Begin Depr Date

Note. One overriding factor that is used to derive the beginning calculation date is that it can never occur before the beginning depreciation date. If according to all calculations it should, it is automatically made to equal the beginning depreciation date.

Asset Management calculates prior period depreciation using the derived beginning calculation date as well as the following items:

• Period Depreciation Allocation

• Accumulated Depreciation

The following examples illustrate how Asset Management calculates prior period depreciation.

Case 1: Add Transactions

The following table shows data that is used in the calculation example that follows it.

Depreciation Results

The following table shows yearly depreciation by period for 1999. Prior period depreciation occurred in periods 7 through 9.

Prior Period Depreciation

Here is the prior period depreciation:

Difference Per Period = Period Depreciation Allocation (allowed) - Depreciation Taken 
Example Period 7: $100 - 0 = $100 
Begin Calc Date = Begin Depr Date 
Periods from Begin Calc Date to Accounting Date = 7, 8, 9 = Periods within 7/1/1999 to 10/1/1999 
Prior Period Depreciation = Sum of Difference Per Period for all periods within Begin Calc Date to Accounting Date 
$300 = $100 + $100 + $100

Case 2: Add Transactions

The following table shows data that is used in the calculation example that follows it.

Depreciation Results

The following table shows yearly depreciation by period for 1999. Prior period depreciation occurred in periods 7 through 9.

Prior Period Depreciation

Here is the prior period depreciation:

Difference Per Period = Period Depreciation Allocation (allowed) - Depreciation Taken
Example Period 7: $100 - 0 = $100
Begin Calc Date = Begin Depr Date
Periods from Begin Calc Date to Accounting Date =
7, 8, 9 = Periods within 7/1/1999 to 10/1/1999
Prior Period Depreciation = Sum of Difference Per Period for all periods within Begin Calc Date to Accounting Date - Accumulated
Depreciation
($200) = ($500) +$100 + $100 + $100

Case 3: Add Transactions

The following table shows data that is used in the calculation example that follows.

Depreciation Results

The following table shows yearly depreciation by period for 1999. Prior period depreciation occurred in periods 3 through 9.

Prior Period Depreciation

Here is the prior period depreciation:

Difference Per Period = Period Depreciation Allocation (allowed) - Depreciation Taken
Example Period 7: $60 - 0 = $60
Begin Calc Date = Begin Depr Date
Periods from In Service Date to Accounting Date =
7, 8, 9, 10= Periods within 3/1/1999 to 10/1/1999
Prior Period Depreciation = Sum of Difference Per Period for all periods within In Service Date to Accounting Date
$420 = $60 + $60 + $60 + $60 + $60 + $60 + $60

Case 4: Add Transactions

The following table shows data that is used in the calculation example that follows it.

Depreciation Results

The following table shows yearly depreciation by period for 1999. Prior period depreciation occurred in periods 3 through 9.

Prior Period Depreciation

Here is the prior period depreciation:

Difference Per Period = Period Depreciation Allocation (allowed) - Depreciation Taken
Example Period 7: $60 - 0 = $60
Begin Calc Date = Begin Depr Date
Periods from In Service to Accounting Date =
3, 4, 5, 6, 7, 8, 9 = Periods within 3/1/1999 to 10/1/1999
Prior Period Depreciation = Sum of Difference Per Period for all periods within In Service Date to Accounting Date
($80) = $60 + $60 + $60 + ($440) + $60 + $60 + $60

Case 5: Add Transactions

The following table shows data that is used in the calculation example that follows it.

Depreciation Results

The following table shows yearly depreciation by period for 1999. Prior period depreciation occurred in periods 7 through 9.

Prior Period Depreciation

Here is the prior period depreciation:

Difference Per Period = Period Depreciation Allocation (allowed) - Depreciation Taken
Example Period 7: $100 - 0 = $100
Begin Calc Date = Begin Depr Date
Periods from Begin Calc Date to Accounting Date =
7, 8, 9 = Periods within 7/1/1999 to 10/1/1999
Prior Period Depreciation = Sum of Difference Per Period for all periods within Begin Calc Date to Accounting Date
$300 = $100 + $100 + $100

Formula-Based Depreciation Methods

Asset Management is equipped to use the following different formula-based depreciation methods:

• Straight Line

• (IND) Straight Line Percent

• Declining Balance with a Switch to Straight Line

• Declining Balance with Depreciation Limit

• Declining Balance

• Flat Rate

• Sum of the Year's Digits

Asset Management can calculate depreciation for each of the first six methods using either a schedule or a formula. The formulas that it uses to calculate yearly depreciation for each of these methods are explained in the following pages.

Straight Line

Yearly Straight Line depreciation is calculated using the following formula:

NBV x (Number of Periods to Depreciate / Remaining Life)

Straight Line Depreciation Example

The following table shows data that is used in the depreciation example that follows.

Depreciation Results

The following table shows yearly depreciation and the calculation that is used to produce the result.

(IND) Straight Line Percent

The Straight Line Percent method that is used in India differs from the Straight Line method. Depreciation is calculated based on rates rather than useful life. In addition, the rates also consider the residual or salvage value at the end of the asset useful life. In India the following assumptions are made:

• Assets are depreciated as of the in-service date.

• The minimum rates that are established by statute depreciate 95 percent of the asset cost over the asset useful life.

• An entity is entitled to depreciate at a higher rate, but not lower.

When using Straight Line Percent as the method, you complete the Percent field with the depreciation rate. The Useful Life field is unavailable. Other fields are ignored for this depreciation calculation. Although residual value is included in the rate, you have to enter salvage value.

Salvage Value acts as a limit. When the NBV reaches this amount, it automatically allocates the rest of the depreciable amount to the last period. Life in Years reflects both years and fractions, such as 8.4. Useful Life and Life in Years are displayed after you save or refresh the page. AM_DEPR_CALC recalculates these fields when it runs. Those assets that are coming from batch processes will calculate only Useful Life and Life in Years when you run AM_DEPR_CALC.

The formula to calculate Useful Life is:

(Cost – Salvage Value) / (Cost x Depr Rate)

For example, an asset that is worth $1000 and a salvage value of $50, with a 4.75% annual depreciation rate, using the actual month convention, will have a useful life of 20 years or 240 periods. Sometimes useful life may result in fractional periods.

Remaining Value and Life to Date

Two different ways are available to calculate depreciation adjustments under Indian Straight Line % Method:

• Remaining Value

• Life to Date

For instance, in the preceding example, suppose that in the sixth year, the rate must change to 5.28 percent because the government adopts a new rate according to Schedule XIV. Using Remaining Value, the system calculates the useful life. It takes into account the new rate on the original cost. It calculates depreciation based on the NBV minus any residual value over the remaining new useful life, where remaining new useful life means the new useful life minus periods that are already depreciated.

Revised Useful Life:

(Cost – Salvage Value) / (Cost x Depr Rate) Revised Useful Life: (1000 – 50) / (1000x.0528) = 17.992424

Rounded up to 18 years or 216 months.

New Depreciation Amount:

(Net Book Value - Limiting Value) / (Revised useful life - Years Depreciated)

New Depreciation Amount:

(762.5 – 50) / (18 – 5) = 54.8076

In the last period, the remaining value will be residual value.

The following table shows the depreciation with the adjustment in the sixth year.

In the case of Life to Date, the useful life is again recalculated. This method takes into account the new rate on the original cost. Depreciation is based on what the system had calculated if the rate would have been the new rate from the beginning. An adjustment to the prior depreciation amounts is required in this method to reflect the change retroactively. It consists of summarizing all depreciation amounts until the change and comparing with the amount that would have been obtained if the asset had always been calculated based on the new rate.

Useful Life:

(Cost – Salvage Value) / (Cost x Depr Rate)

Useful Life:

(1000 – 50) / (1000 x .0528) = 17.992424

Rounded up to 18 years or 216 months.

The following table depicts the depreciation if the rate had always been 5.28 percent.

Compare the preceding table that shows what the amount would have been with a constant rate of 5.28 percent versus the following table that shows what the amounts are with a change and an adjustment in the sixth year.

Adjustment PDP:

Total Depreciation at new rate – Total Depreciation at former rate

Adjustment PDP:

264 – 237.50 = 26.50 for the first 5 years.

New Depreciation Amount:

(Net Book Value – Adj PDP - Limiting Value) / (Revised useful life – Years Depreciated)

New Depreciation Amount:

(762.5 – 26.5 - 50) / (18 – 5) = 52.7692

Declining Balance with a Switch to Straight Line

Declining Balance with a Straight Line Switch performs two simultaneous equations to calculate yearly depreciation. One equation calculates declining balance depreciation and the other calculates straight line depreciation. Asset Management then compares the two yearly depreciation amounts and applies whichever is greater.

Note that in this type of calculation the asset’s net book value is multiplied by the declining balance percentage times the straight line depreciation percentage.

NBV x ((Number of Periods to Depreciate / Life) x DB%)

Declining Balance with a Switch to Straight Line Example

The following table shows data that is used in the depreciation example that follows it.

Depreciation Results

The following table shows yearly depreciation and the calculation that is used to produce the result.

In this example, in 1998, the straight line depreciation is greater than the declining balance depreciation. Therefore, switch to straight line depreciation. The declining balance calculation for 1998 is 1728 x ((12/60) x (200/100)) = 691.20. In 1999, the straight line depreciation is equal to the declining balance depreciation.

Declining Balance with Depreciation Limit

This calculation type enables you to specify annual depreciation limits based on a percentage of an asset’s cost. This method supports asset management practices that are commonly used in some European countries. In environments in which this is legally acceptable, the advantage to this method is that it provides greater decreases in value in the first years of an asset’s service. In some environments, a company may use this depreciation method initially and then switch to straight-line when that method provides a greater write-off.

This method runs three calculations and performs comparisons between the results.

First, it calculates using the formula that is already documented for Declining Balance with a Switch to Straight Line:

NBV x ( (Number of Periods to Depreciate/Life) x DB% )

(See DB column in the table provided with the following example.)

It then calculates using the specified limit percentage of original cost or bet book value:

NBV x Limit%

(See MAX column in the table provided with the following example.)

The results of these two calculations are compared and the system determines which amount is lesser. (See Comparison 1 column in the table provided with following example.)

Finally, it calculates using the Straight Line formula:

NBV x (Number of Periods to Depreciate/Remaining Life)

(See SL column in the table provided with following example.)

Results of the Straight Line calculation are compared with the lessor amount from the first comparison. (Column SL compared with column Comparison 1 in the following table. Comparison 2 column shows when the Straight Line method produces the greater result.)

The greater amount between this final comparison is the annual depreciation amount. (See Depr column in the table after the following table.)

Declining Balance with Depreciation Limit Example

The following table shows data that is used in the depreciation example that follows it.

Depreciation Results

The following table shows yearly depreciation and the calculation that is used to produce the result.

Declining Balance

For this type of calculation, the declining balance percentage represents a percentage of NBV.

NBV x DB%

When you are depreciating an asset with a declining balance method, the life of the asset is irrelevant. Note that if you used this method alone, an asset would never be fully depreciated. To fully depreciate an asset using the Declining Balance method, you must enter either a book low limit or an end depreciation date. When an asset’s NBV reaches its book low limit or end depreciation date, the remaining value is taken in depreciation for that year.

Declining Balance Example

The following table shows data that is used in the depreciation example that follows it.

Depreciation Results

The following table shows yearly depreciation and the calculation that is used to produce the result.

Calculations continue in this manner until the book low limit or end depreciation date is reached. If no book low limit or end depreciation date is specified, the asset never fully depreciates.

Flat Rate

The formula for calculating Flat Rate depreciation is simple.

BasisxFlat %

Flat Rate with an Averaging Option

You can combine the Flat Rate depreciation method with either a monthly or yearly averaging option. These options are typically used by utility companies to depreciate composite assets. When these options are used, Asset Management uses up to three separate formulas to calculate depreciation for adjustments—one for calculating current period depreciation, one for calculating following period depreciation, and one for calculating depreciation for all subsequent periods.

These formulas are used only for calculating additional depreciation resulting from adjustments to the average balance. And these adjustments are applied only to the current year. For all subsequent years, as well as the first time it is done, the system calculates depreciation by applying the flat rate percentage to the average balance and allocating this amount among the periods.

Because of the averaging option, all adjustment transactions must take effect from the beginning of the year to its end. Therefore, current period depreciation is calculated after each transaction on a year-to-date basis.

As adjustments are made, additional depreciation is posted for each period that is affected.

Note. Using the flat rate depreciation method causes any depreciation to be posted to the end of the calendar. If this is not your intention, you must enter a low limit of .01 when you first select the depreciation method on the Asset Book Definition page group for this asset. If you have not already done this, update the Depreciation Method field on the General 2 page by selecting Flat Rate and entering .01 in the Low Limit additional field that appears.

Monthly Averaging Option

Review the following examples of monthly averaging calculations resulting from a $2000 adjustment made in period 3. The asset is depreciated at 12%.

((Adjustment Amount / 2) x Flat Rate %) x Period Allocation

Calculation for the current period (YTD):

(($2000 USD / 2) x 12%) x 3/12 = $30 USD

Current Period Depreciation + ((Adjustment Amount x Flat Rate %) x Period Allocation)

Calculation for the following period:

$30 USD + (($2000 USD x 12%) x 1/12) = $50 USD

(Adjustment Amount x Flat Rate %) x Period Allocation

Calculation for Subsequent Periods:

($2000 USDx12%) x 1/12 = $20 USD

Note. The only exception to this rule occurs when the following period crosses into another fiscal year. When this is the case, all periods but the current one are calculated using the full value of the transaction. Current Period depreciation is not added to the following period depreciation.

Yearly Averaging Option

When using the yearly averaging option, you’ll want to estimate financial activity for the year. The original estimate should be posted as an add transaction in the first period of the year and subsequently adjusted as the actual figures become available.

Review the following example of the yearly averaging option using the same $2000 adjustment in Period 3. The asset is depreciated at 12 percent.

(( Adjustment Amount / 2) x Flat Rate %) x Period Allocation

Calculation for the current period (YTD):

(($2000 USD / 2) x 12%) x 3/12 = $30 USD

((Adjustment Amount / 2) x Flat Rate %) x Period Allocation

Calculation for all subsequent periods:

(($2000 USD / 2) x 12%) x 1/12 = $10 USD

Sum of the Years’ Digits

Yearly Sum of the Years’ Digits depreciation is calculated using the following formula:

(( Remaining Years of Life / Sum of Years Remaining) x NBV) x % of Year to Depreciate

Sum of the Years Digits Example

The following table shows data that is used in the depreciation example that follows it.

Depreciation Results

The following table shows yearly depreciation and the calculation that is used to produce the result.

Calculation for the first year Sum of Years Remaining = 3/(1+2+3)

Units of Production

Units of production depreciation differs from other methods in that it does not depreciate an asset based on its periods of life, but rather on its production detail. In this method, an asset is assumed to have a fixed lifetime production capacity—a maximum number of units it can produce. Thus, a fixed amount of depreciation is allotted to each unit of production. The net book value of the asset is then multiplied by the number of units that are produced in a period over the remaining units to be produced to determine how much depreciation to take for that period.

NBV x (Units Produced / Units Remaining)

Production detail for the asset is entered into the Units of Production table (Set Up Financials/Supply Chain, Product Related, Asset Management, Depreciation, Units of Production). Each time new detail is added to this table, open transactions are created for each asset that is associated with it. You should recalculate depreciation each time you add to or change the detail in the Units of Production table.

Units of Production Example

The following table shows data that is used in the depreciation example that follows it.

Depreciation Results

The following table shows yearly and monthly depreciation and the calculation that is used to produce the result.

Note. Units remaining are calculated by summing the production units for all remaining periods that are set up on the Units of Production page (Set Up Financials/Supply Chain, Product Related, Asset Management, Depreciation, Units of Production).